本文是笔者的机器学习笔记,学习课程为吴恩达老师的公开课(网上搬运资源很多此处不附链接了),供大家学习参考
此为第一部分,第二部分见Fundamentals of Machine Learning 2
机器学习概述
基本概念
机器学习是一门在没有明确编程的情况下让计算机学习的科学,已成长为人工智能的子领域,研究能使机器模拟人类根据经验学习的算法。
主要算法类型
- 监督学习(Supervised Learning):通过给定输入与对应正确输出标签(输入 - 输出对),让算法学习输入到输出的映射关系,最终能对全新输入给出合理准确的预测。
- 非监督学习(Unsupervised Learning):仅使用无标签的输入数据,算法需自行从数据中发现结构或模式。
- 强化学习(Reinforcement Learning):智能体(Agent)以试错方式学习,通过与环境交互获得奖赏指导行为,目标是使智能体获得最大奖赏,无需预先给定数据,依赖环境对动作的奖励反馈更新模型参数。
监督学习(Supervised Learning)
核心逻辑
- 映射关系:学习输入(x)到输出(y)的映射(x→y),通过输入示例与对应正确答案(标签)训练模型,最终对新输入产生适当输出。
- 典型应用:垃圾邮件识别、销售预测、机器翻译等。
两大核心任务
回归(Regression)
-
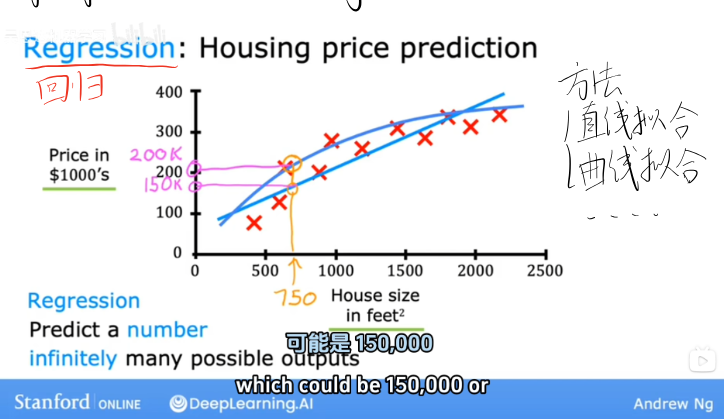
定义:预测连续的数值型输出,可能的输出有无限多个。
-
示例:房屋价格预测
通过房屋面积(输入 x,单位:平方英尺)预测房屋价格(输出 y,单位:千美元),通过直线拟合数据建立模型,例如预测某 750 平方英尺的房屋价格可能为 150,000 美元。
-
数据示例:
| 房屋面积(平方英尺) | 价格(千美元) |
|---|---|
| 2104 | 400 |
| 1416 | 232 |
| 1534 | 315 |
| 852 | 178 |
| 3210 | 870 |
分类(Classification)
-
定义:预测离散的类别型输出,可能的输出是有限的小集合(如 0、1、2 等)。
-
示例:乳腺癌检测
输入肿瘤直径、患者年龄、细胞形状均匀度、边界特征等,预测肿瘤为良性(benign,如标签 0)或恶性(malignant,如标签 1 或 2),通过拟合边界线区分不同类别。
-
多输入情形:实际问题中常存在多个输入特征,例如通过 “年龄(Age)+ 肿瘤大小(Tumor size)” 共同预测肿瘤良恶性,是机器学习的常态。
监督学习小结
| 任务类型 | 输出特点 | 核心目标 |
|---|---|---|
| 回归 | 连续数值,无限多个可能输出 | 预测准确的数值结果 |
| 分类 | 离散类别,有限个可能输出 | 预测正确的类别归属 |
非监督学习(Unsupervised Learning)
核心逻辑
- 仅使用无标签的输入数据(仅 x,无 y),算法自主挖掘数据中的结构或模式。
- 与监督学习的关键区别:无需预先给定 “正确答案”(标签),从无标签数据中学习。
典型任务
聚类(Clustering)
-
定义:将无标签数据自动分组到不同簇(clusters),相似数据点归为同一簇。
-
示例:Google 新闻分类
通过新闻关键词自动将当天新闻划分为不同主题(如 “体育”“科技”“财经”)。
降维(Dimensionality Reduction)
- 定义:将高维大数据集压缩为低维数据集,同时尽可能减少信息丢失,便于数据可视化或后续处理。
异常检测(Anomaly Detection)
- 定义:从数据中找出不寻常的数据点(异常值),例如信用卡欺诈交易检测、设备故障检测等。
机器学习术语(Machine Learning Terminology)
| 术语 | 定义 |
|---|---|
| 输入变量(x) | 用于预测的特征(如房屋面积、肿瘤大小),也叫 “特征(Feature)” |
| 输出变量(y) | 待预测的结果(如房屋价格、肿瘤良恶性),也叫 “目标变量(Target)” |
| 训练集(Training Set) | 用于训练模型的数据集合,包含多个训练样本 |
| 训练样本数(m) | 训练集中样本的总数(如 m=47 表示有 47 个训练样本) |
| 单个训练样本(x⁽ⁱ⁾, y⁽ⁱ⁾) | 第 i 个训练样本的输入(x⁽ⁱ⁾)与对应输出(y⁽ⁱ⁾),如 (x⁽¹⁾, y⁽¹⁾)=(2104, 400) |
| 特征数(n) | 每个训练样本包含的特征数量(如房屋预测中 “面积 + 卧室数 + 楼层”,n=3) |
| 模型(f) | 输入到输出的映射函数,也叫 “假设(Hypothesis)”,如 f (x)=wx+b |
| 预测值 ŷ | 模型根据给定输入推测的预测值 |
线性回归模型(Linear Regression Model)
基本定义
- 监督学习中的回归任务模型,通过拟合一条直线(或高维空间中的超平面)建立输入与输出的线性关系,用于预测连续数值。
- 注意:线性回归是回归模型的一种,所有能预测数值的监督学习模型都可解决回归问题。
模型表达式
一元线性回归(单特征)
-
仅含一个输入特征(x),模型公式:$f_{w,b}(x) = wx + b$
其中,
w为权重(weight),b为偏置(bias),$f_{w,b}(x)$ 也记为ŷ(预测值),y为训练集中的真实值。
多元线性回归(多特征)
-
含多个输入特征$(x_1, x_2, …, x_n)$,模型公式:$f_{\vec{w}, b}(\vec{x}) = w_1x_1 + w_2x_2 + … + w_nx_n + b$
其中,$\vec{w} = [w_1, w_2, …, w_n]$ 为权重向量,$\vec{x} = [x_1, x_2, …, x_n] $为特征向量,可通过向量点积简化为:$f_{\vec{w}, b}(\vec{x}) = \vec{w} \cdot \vec{x} + b$
-
多特征数据示例:
| 房屋面积(x₁) | 卧室数(x₂) | 楼层数(x₃) | 房龄(x₄) | 价格(千美元) |
|---|---|---|---|---|
| 2104 | 5 | - | 45 | 460 |
| 1416 | 3 | 2 | 40 | 232 |
| 1534 | 3 | 2 | 30 | 315 |
| 852 | 2 | 1 | 36 | 178 |
向量化(Vectorization)
-
作用:减少代码量,利用 NumPy 等工具调用并行硬件,大幅提升计算速度,尤其适用于大规模数据集。
-
示例:
-
无向量化(循环计算):
$f = w[0]x[0] + w[1]x[1] + w[2]x[2] + b$
向量化(直接点积):
$f = np.dot(w, x) + b$
代价函数(Cost Function)
核心作用
- 衡量模型预测值$\hat{y} = f_{w,b}(x))$与,真实值$(y)$的差异即模型对训练数据的拟合程度。
- 目标:找到最优的 $w $和 $b$,使代价函数值最小。
常用代价函数:平方误差代价函数(Squared Error Cost Function)
公式(线性回归)
-
对于 m 个训练样本,
-
代价函数为:
$J(w,b) = \frac{1}{2m} \sum_{i=1}^{m} \left( f_{w,b}(x^{(i)}) - y^{(i)} \right)^2$
其中,$\frac{1}{2}$是为了后续求导计算简洁,不影响最小值的位置。
逻辑回归的代价函数
直观理解
-
简化场景(固定 b=0,仅分析 w):
当
w=1时,预测值与真实值差异较小,代价函数值较小;当w=0或w=-0.5时,差异增大,代价函数值升高。 -
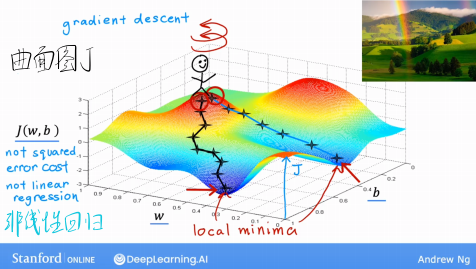
三维可视化(含 w 和 b):以
w和b为坐标轴,代价函数值J(w,b)为高度,形成三维曲面,曲面最低点对应最优参数。 -
等值线图(等高线):
二维平面上,同一等值线的
J(w,b)值相同,中心处值最小,对应最优参数。
逻辑回归的代价函数
-
由于逻辑回归输出为 0-1 概率,平方误差代价函数会导致非凸函数(存在多个局部最小值),故采用对数损失函数(Log Loss):
-
单个样本损失:$L(f_{w,b}(x^{(i)}), y^{(i)}) = \begin{cases} -log(f_{w,b}(x^{(i)})) & \text{if } y^{(i)}=1 \ -log(1-f_{w,b}(x^{(i)})) & \text{if } y^{(i)}=0 \end{cases}$
-
整体代价函数:
$J(w,b) = -\frac{1}{m} \sum_{i=1}^{m} \left[ y^{(i)}log(f_{w,b}(x^{(i)})) + (1-y^{(i)})log(1-f_{w,b}(x^{(i)})) \right]$
-
-
特点:凸函数,梯度下降可找到全局最小值。
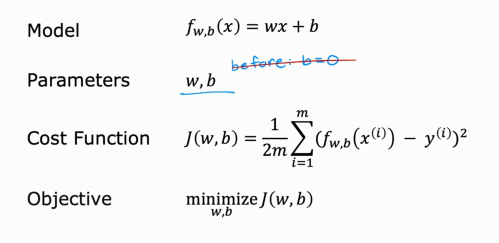
梯度下降(Gradient Descent)
基本定义
- 一种通用的优化算法,用于最小化任意代价函数(不仅限于线性回归或逻辑回归),广泛应用于机器学习领域。
- 核心思想:从初始参数(如 w=0,b=0)出发,通过不断调整参数(w 和 b),沿代价函数梯度下降方向减小 J(w,b),直至收敛到局部最小值(或接近最小值)。
算法步骤
-
初始化参数:设定初始 w 和 b(如均为 0)。
-
迭代更新:
同时更新 w 和b(关键:不能分步更新),公式为:
$tmp_w = w - \alpha \cdot \frac{\partial J(w,b)}{\partial w}$
$tmp_b = b - \alpha \cdot \frac{\partial J(w,b)}{\partial b}$
$w = tmp_w, \quad b = tmp_b$
-
终止条件:当$ J(w,b) $不再明显减小(收敛)时停止。
关键参数:学习率(α)
-
作用:决定每一步更新参数的步幅大小。
-
影响:
- α 过小:迭代次数多,收敛慢。
- α 过大:可能跨越最小值,导致 $J(w,b) $震荡甚至发散(不收敛)。
-
选择建议:尝试 3 倍递增的取值(如 0.001、0.003、0.01、0.03、0.1…),找到使 J(w,b) 快速下降的合适值。
线性回归的梯度下降
-
偏导数计算(代入平方误差代价函数):
$\frac{\partial J(w,b)}{\partial w} = \frac{1}{m} \sum_{i=1}^{m} \left( f_{w,b}(x^{(i)}) - y^{(i)} \right)x^{(i)}$
$\frac{\partial J(w,b)}{\partial b} = \frac{1}{m} \sum_{i=1}^{m} \left( f_{w,b}(x^{(i)}) - y^{(i)} \right)$
-
特点:线性回归的代价函数是凸函数,梯度下降一定能找到全局最小值(无局部最小值问题)。
逻辑回归的梯度下降
-
偏导数计算(代入对数损失函数):
形式与线性回归相同但 \(f_{w,b}(x) = g(w \cdot x + b)\)(\(g(z)\) 为 sigmoid 函数),故实际计算不同:
$\frac{\partial J(w,b)}{\partial w_j} = \frac{1}{m} \sum_{i=1}^{m} \left( f_{w,b}(x^{(i)}) - y^{(i)} \right)x_j^{(i)}$
$\frac{\partial J(w,b)}{\partial b} = \frac{1}{m} \sum_{i=1}^{m} \left( f_{w,b}(x^{(i)}) - y^{(i)} \right)$
逻辑回归(Logistic Regression)
基本定义
- 虽名为 “回归”,但实际是解决二分类问题的算法,输出为样本属于某一类别的概率(0~1 之间)。
- 核心:通过 sigmoid 函数将线性模型的输出(z=w⋅x+b)映射到 0~1 区间。
Sigmoid 函数(逻辑函数)
- 公式:$g(z) = \frac{1}{1 + e^{-z}}$
- 性质:
- 当 z≥0 时,g(z)≥0.5
- 当 z<0 时,g(z)<0.5
- 输出范围:0<g(z)<1
模型表达式
-
逻辑回归模型:$f_{w,b}(x) = g(w \cdot x + b) = \frac{1}{1 + e^{-(w \cdot x + b)}}$
-
输出含义:
$=P(y=1∣x;w,b)$
,即给定输入 x 和参数 w、b 时,样本属于类别 1(正类)的概率。
示例:若$f_{w,b}=0.7$,表示该样本有 70% 概率为正类(如恶性肿瘤),30% 概率为负类(如良性肿瘤)。
决策边界(Decision Boundary)
- 定义:划分正类(y=1)和负类(y=0)的边界,由$ f_{w,b}(x)=0.5$ 推导而来(此时 z=w⋅x+b=0)。
- 类型:
- 线性决策边界:当特征为线性组合时(如$ w_1x_1 + w_2x_2 + b = 0$),边界为直线(二维)或平面(高维)。
- 非线性决策边界:通过特征工程(如添加多项式特征$ x_1^2, x_1x_2 $等),可拟合圆形、椭圆形等非线性边界,适用于复杂数据分布。
模型优化:特征工程与正则化
特征工程(Feature Engineering)
- 定义:根据问题直觉,通过变换、合并或创建新特征,提升模型预测能力。
- 示例:
- 房屋预测中,将 “房屋正面宽度(frontage)” 和 “深度(depth)” 合并为 “面积(area = frontage × depth)”,面积对价格的预测更直接。
- 多项式回归:将特征 x 扩展为 x,x2,x3 等,拟合非线性数据(需配合特征缩放)。
特征缩放(Feature Scaling)
-
目的:使不同取值范围的特征(如 “房屋面积:300
2000 平方英尺”“卧室数:05”)具有相似的数值范围(通常目标 −1≤x**j≤1,可接受 −3≤x**j≤3),加速梯度下降收敛。 -
常用方法:
-
归一化(Normalization):归一化(Normalization):
$x_j^{scaled} = \frac{x_j - min(x_j)}{max(x_j) - min(x_j)}$
将特征缩放到 0~1 区间。
-
标准化(Z-score Normalization):$x_j^{scaled} = \frac{x_j - \mu_j}{\sigma_j}$,
其中$ \mu_j$ 为特征j的均值,$\sigma_j $为标准差,使特征均值为 0、标准差为 1。
-
正则化(Regularization)
问题背景:过拟合(Overfitting)与欠拟合(Underfitting)
- 欠拟合:模型过于简单,无法拟合训练数据(高偏差,high bias),如用直线拟合非线性数据。
- 过拟合:模型过于复杂,完美拟合训练数据但泛化能力差(高方差,high variance),如用四阶多项式拟合少量线性数据。
正则化核心思想
- 通过在代价函数中添加正则项,惩罚过大的参数值(w**j),使模型参数尽可能小,从而简化模型,避免过拟合(不惩罚 b,影响较小)。
常用正则化方法:L2 正则化(权重衰减)
-
线性回归的正则化代价函数:$J(w,b) = \frac{1}{2m} \sum_{i=1}^{m} \left( f_{w,b}(x^{(i)}) - y^{(i)} \right)^2 + \frac{\lambda}{2m} \sum_{j=1}^{n} w_j^2$
-
逻辑回归的正则化代价函数:
-
$J(w,b) = -\frac{1}{m} \sum_{i=1}^{m} \left[ y^{(i)}log(f_{w,b}(x^{(i)})) + (1-y^{(i)})log(1-f_{w,b}(x^{(i)})) \right] + \frac{\lambda}{2m} \sum_{j=1}^{n} w_j^2$
-
正则化参数 λ:
-
λ=0:无正则化,可能过拟合。
- λ 过大:惩罚过强,参数趋近于 0,模型过于简单,导致欠拟合。
-
选择:需通过验证集调整,找到平衡过拟合与欠拟合的最优值。
正则化的梯度下降更新
-
线性回归(以\(w_j\)为例):
$w_j = w_j - \alpha \left[ \frac{1}{m} \sum_{i=1}^{m} \left( f_{w,b}(x^{(i)}) - y^{(i)} \right)x_j^{(i)} + \frac{\lambda}{m}w_j \right]$
-
其中,$1 - \alpha \cdot \frac{\lambda}{m} $项使\(w_j\)每次更新时 “收缩”,实现权重衰减。
-
逻辑回归(更新公式形式与线性回归相同,仅$ f (x) $计算不同)。
过拟合的其他解决方法
- 收集更多训练数据:增加数据量可提升模型泛化能力,是解决过拟合的有效方法(前提是数据质量高)。
- 减少特征数量:通过特征选择(如手动筛选或算法自动选择),剔除无关或冗余特征,简化模型(缺点:可能丢失有用信息)。
